 Some Basic Properties
Some Basic Properties
 Some Basic Properties
Some Basic Properties
To start out with, let us note that the limit, when it exists, is
unique. That is why we say "the limit", not "a limit". This
property translates formally into:
Most of the examples studied before used the definition of the
limit. But in general it is tedious to find the ![]() given
the
given
the
![]() .
The following properties help circumvent this.
.
The following properties help circumvent this.
Theorem. Let f(x) and g(x) be two functions. Assume
that
These properties are very helpful. For example, it is easy to
check that
The next natural question then is to ask what happens to quotients of functions. The following result answers this question:
Theorem. Let f(x) and g(x) be two functions. Assume
that
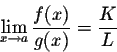
This implies immediately the following:
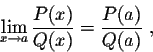
Example. Assume that
Answer. Note that we cannot apply the result about limits of
quotients directly, since the limit of the denominator is zero.
The following manipulations allow to circumvent this problem. We
have
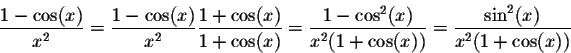
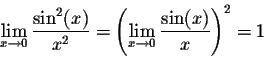
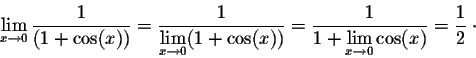
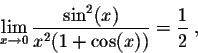
Exercise 1. Find the limit
Exercise 2. Evaluate
Let us continue to list some basic properties of limits.
Theorem. Let f(x) be a positive function, i.e.
This is actually a special case of the following general result
about the composition of two functions:
Theorem. Let f(x) and g(x) be two functions. Assume
that
Example. Geometric considerations imply
Using the trigonometric identities
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.
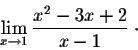
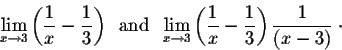
![]() .
Assume that
.
Assume that
![]()
Then
![]()
![]()
Then
![]()
![]()
Since
![]() for x close to 0, then we have
for x close to 0, then we have
![]()
which implies
![]()
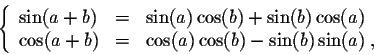
we obtain
![]()
 S.O.S MATHematics home page
S.O.S MATHematics home page
Helmut Knaust
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour