Product and Sum Formulas Product and Sum Formulas
From the Addition Formulas, we derive the following trigonometric formulas (or identities)
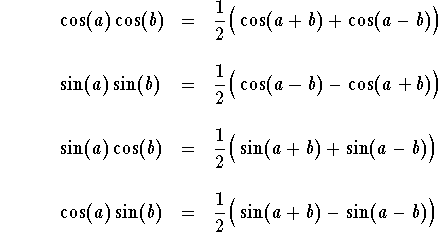
Remark. It is clear that the third formula and the fourth are equivalent (use the property 
to see it).
The above formulas are important whenever need rises to transform the product of sine and cosine into a sum. This is a very useful idea in techniques of integration.
Example. Express the product 
as a sum of trigonometric functions.
Answer. We have
which gives
Note that the above formulas may be used to transform a sum into a product via the identities
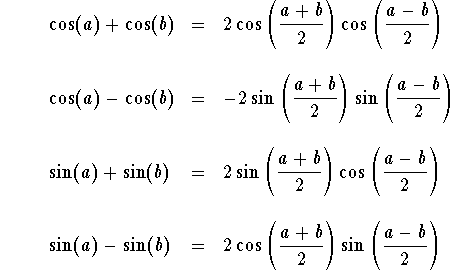
Example. Express 
as a product.
Answer. We have
Note that we used 
.
Example. Verify the formula
Answer. We have
and
Hence
which clearly implies
Example. Find the real number x such that 
and
Answer. Many ways may be used to tackle this problem. Let us use the above formulas. We have
Hence
Since , the equation 
gives 
and the equation 
gives 
. Therefore, the solutions to the equation
are
Example. Verify the identity
Answer. We have
Using the above formulas we get
Hence
which implies
Since 
, we get
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Mohamed A. Khamsi