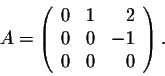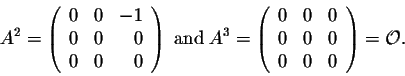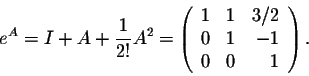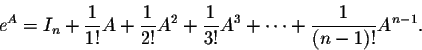Matrix Exponential
Matrix Exponential

The matrix exponential plays an important role in solving system of linear differential equations. On this page, we will define such an object and show its most important properties. The natural way of defining the exponential of a matrix is to go back to the exponential function ex and find a definition which is easy to extend to matrices. Indeed, we know that the Taylor polynomials
converges pointwise to ex and uniformly whenever x is bounded. These algebraic polynomials may help us in defining the exponential of a matrix. Indeed, consider a square matrix A and define the sequence of matrices
When n gets large, this sequence of matrices get closer and closer to a certain matrix. This is not easy to show; it relies on the conclusion on ex above. We write this limit matrix as eA. This notation is natural due to the properties of this matrix. Thus we have the formula
One may also write this in series notation as
At this point, the reader may feel a little lost about the definition above. To make this stuff clearer, let us discuss an easy case: diagonal matrices.
Example. Consider the diagonal matrix
It is easy to check that
for
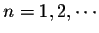 .
Hence we have
.
Hence we have
Using the above properties of the exponential function, we deduce that
Indeed, for a diagonal matrix A, eA can always be obtained by replacing the entries of A (on the diagonal) by their exponentials. Now let B be a matrix similar to A. As explained before, then there exists an invertible matrix P such that
B = P-1AP.
Moreover, we have
Bn = P-1AnP
for
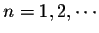 ,
which implies
,
which implies
This clearly implies that
In fact, we have a more general conclusion. Indeed, let A and B be two square matrices. Assume that 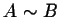 .
Then we have
.
Then we have
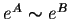 .
Moreover, if
B = P-1AP, then
.
Moreover, if
B = P-1AP, then
eB = P-1eAP.
Example. Consider the matrix
This matrix is upper-triangular. Note that all the entries on the diagonal are 0. These types of matrices have a nice property. Let us discuss this for this example. First, note that
In this case, we have
In general, let A be a square upper-triangular matrix of order n. Assume that all its entries on the diagonal are equal to 0. Then we have
Such matrix is called a nilpotent matrix. In this case, we have
As we said before, the reasons for using the exponential notation for matrices reside in the following properties:
Theorem. The following properties hold:
- 1.
-
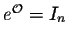 ;
;
- 2.
- if A and B commute, meaning AB = BA, then we have
eA+B = eAeB;
- 3.
- for any matrix A, eA is invertible and

[Geometry]
[Algebra]
[Trigonometry ]
[Calculus]
[Differential Equations]
[Matrix Algebra]
 S.O.S MATH: Home Page
S.O.S MATH: Home Page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Author: M.A. Khamsi
Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
 Matrix Exponential
Matrix Exponential Matrix Exponential
Matrix Exponential
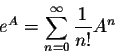
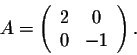
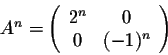
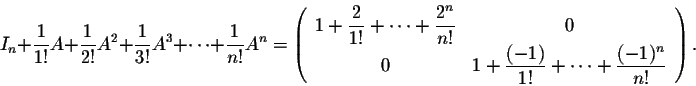
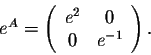
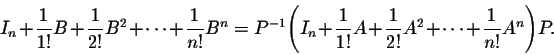
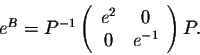
![]() .
Then we have
.
Then we have
![]() .
Moreover, if
B = P-1AP, then
.
Moreover, if
B = P-1AP, then