Eigenvalues and Eigenvectors: An Introduction

The eigenvalue problem is a problem of considerable theoretical interest and wide-ranging application. For example, this problem is crucial in solving systems of differential equations, analyzing population growth models, and calculating powers of matrices (in order to define the exponential matrix). Other areas such as physics, sociology, biology, economics and statistics have focused considerable attention on "eigenvalues" and "eigenvectors"-their applications and their computations. Before we give the formal definition, let us introduce these concepts on an example.

Example. Consider the matrix

$$A = \left(\begin{array}{rrr} 1&2&1\\ 6&-1&0\\ -1&-2&-1\\ \end{array}\right).$$

Consider the three column matrices

$$C_1 = \left(\begin{array}{rrr} 1\\ 6\\ -13\\ \end{array}\r... ... = \left(\begin{array}{rrr} 2\\ 3\\ -2\\ \end{array}\right).$$

We have

$$AC_1 = \left(\begin{array}{rrr} 0\\ 0\\ 0\\ \end{array}\ri... ... = \left(\begin{array}{rrr} 6\\ 9\\ -6\\ \end{array}\right).$$

In other words, we have

$$AC_1 = 0 C_1,\; AC_2 = -4 C_2,\; \;\mbox{and}\;\; AC_3 = 3 C_3.$$

Next consider the matrix P for which the columns are C₁, C₂, and C₃, i.e.,

$$P = \left(\begin{array}{rrr} 1&-1&2\\ 6&2&3\\ -13&1&-2\\ \end{array}\right).$$

We have det(P) = 84. So this matrix is invertible. Easy calculations give

$$P^{-1} = \frac{1}{84} \left(\begin{array}{rrr} -7&0&-7\\ -27&24&9\\ 32&12&8\\ \end{array}\right).$$

Next we evaluate the matrix P^-1AP. We leave the details to the reader to check that we have

$$\frac{1}{84} \left(\begin{array}{rrr} -7&0&-7\\ -27&24&9\\ ... ...gin{array}{rrr} 0&0&0\\ 0&-4&0\\ 0&0&3\\ \end{array}\right).$$

In other words, we have

$$P^{-1}AP = \left(\begin{array}{rrr} 0&0&0\\ 0&-4&0\\ 0&0&3\\ \end{array}\right).$$

Using the matrix multiplication, we obtain

$$A = P \left(\begin{array}{rrr} 0&0&0\\ 0&-4&0\\ 0&0&3\\ \end{array}\right)P^{-1}$$

which implies that A is similar to a diagonal matrix. In particular, we have

$$A^{n} = P \left(\begin{array}{rrr} 0&0&0\\ 0&(-4)^n&0\\ 0&0&3^n\\ \end{array}\right)P^{-1}$$

for $n=1,2,\cdots$. Note that it is almost impossible to find A⁷⁵ directly from the original form of A.

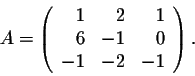
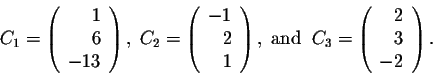
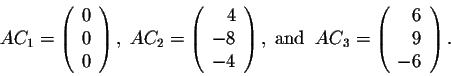
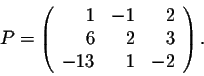
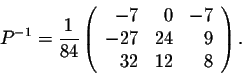
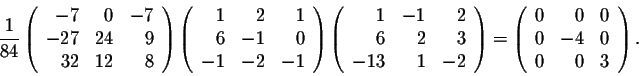
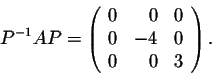
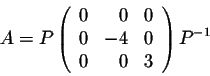
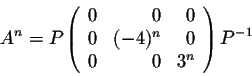
This example is so rich of conclusions that many questions impose themselves in a natural way. For example, given a square matrix A, how do we find column matrices which have similar behaviors as the above ones? In other words, how do we find these column matrices which will help find the invertible matrix P such that P^-1AP is a diagonal matrix?

From now on, we will call column matrices vectors. So the above column matrices C₁, C₂, and C₃ are now vectors. We have the following definition.

Definition. Let A be a square matrix. A non-zero vector C is called an eigenvector of A if and only if there exists a number (real or complex) $\lambda$ such that

$$A C = \lambda C.$$

If such a number $\lambda$ exists, it is called an eigenvalue of A. The vector C is called eigenvector associated to the eigenvalue $\lambda$.

Remark. The eigenvector C must be non-zero since we have

$$A {\cal O} = {\cal O} = \lambda {\cal O}$$

for any number $\lambda$.

Example. Consider the matrix

$$A = \left(\begin{array}{rrr} 1&2&1\\ 6&-1&0\\ -1&-2&-1\\ \end{array}\right).$$

We have seen that

$$AC_1 = 0 C_1,\; AC_2 = -4 C_2,\; \;\mbox{and}\;\; AC_3 = 3 C_3$$

where

$$C_1 = \left(\begin{array}{rrr} 1\\ 6\\ -13\\ \end{array}\r... ... = \left(\begin{array}{rrr} 2\\ 3\\ -2\\ \end{array}\right).$$

So C₁ is an eigenvector of A associated to the eigenvalue 0. C₂ is an eigenvector of A associated to the eigenvalue -4 while C₃ is an eigenvector of A associated to the eigenvalue 3.

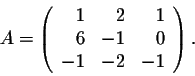
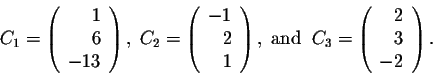
It may be interesting to know whether we found all the eigenvalues of A in the above example. In the next page, we will discuss this question as well as how to find the eigenvalues of a square matrix.

[Geometry] [Algebra] [Trigonometry ] [Calculus] [Differential Equations] [Matrix Algebra]

S.O.S MATH: Home Page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: M.A. Khamsi

Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour