 Bessel's Inequality and Parseval's Formula: The Energy Theorem
Bessel's Inequality and Parseval's Formula: The Energy Theorem Bessel's Inequality and Parseval's Formula: The Energy Theorem
Bessel's Inequality and Parseval's Formula: The Energy Theorem
We have seen some types of approximations, such as Taylor and Fourier approximations. The type of convergence
used changes depending on the nature of the approximation. One of the most useful for Fourier approximations is
L2-convergence:
Let f (x) be an integrable function on the interval
[- ![]() ,
,![]() ], such that
], such that
Theorem. Bessel's Inequality Let f (x) be a
function defined on
[- ![]() ,
,![]() ] such that f2(x) has a finite
integral on
[-
] such that f2(x) has a finite
integral on
[- ![]() ,
,![]() ]. If an and bn are the Fourier
coefficients of the function f (x), then we have
]. If an and bn are the Fourier
coefficients of the function f (x), then we have
Remark. The quantity
An = ![]() is called the amplitude of the nth harmonic.
The square of the amplitude has a useful interpretation. Indeed, borrowing terminology from the study of periodic waves, we define the energy E of a 2
is called the amplitude of the nth harmonic.
The square of the amplitude has a useful interpretation. Indeed, borrowing terminology from the study of periodic waves, we define the energy E of a 2![]() -periodic function f (x) to be the number
-periodic function f (x) to be the number
You may ask the following question: when does the inequality become an equality?
Note that for Fourier polynomials, the inequality does indeed become an equality. Using this, one can show that the answer to the question is in the affirmative if and only if
Theorem. Parseval's Formula or the Energy Theorem. Let
f (x) be a function defined on
[- ![]() ,
,![]() ] such that f2(x)
has a finite integral on
[-
] such that f2(x)
has a finite integral on
[- ![]() ,
,![]() ]. If an and bn are
the Fourier coefficients of f (x), then we have
]. If an and bn are
the Fourier coefficients of f (x), then we have
Remark. One may wonder when does Parseval's Formula hold? This is the case, for example, for piecewise smooth functions. The reason behind is the uniform convergence of the Fourier partial sums to f (x), ie.
Application: Least Square Error.
One application of Parseval's Formula is the measure of the least square error
![]() defined by
defined by
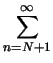 (a2n + b2n).
(a2n + b2n).
Example. Let
f (x) = | x| be defined on
[- ![]() ,
,![]() ]. Find
]. Find
![]() and its asymptotic behavior when N gets large.
and its asymptotic behavior when N gets large.
Answer. Since f (x) is even, we have bn = 0. On the other hand, easy calculations give
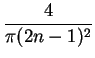 .
.
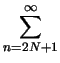
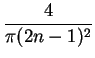
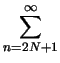
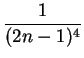 .
.
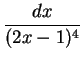 =
= 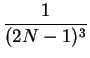 ,
,
Recall that the sequences {un} and {vn} satisfy

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: M.A. Khamsi