Equilibrium Point Analysis: Linearization Technique

Recall that only the solutions of linear systems may be found explicitly. The problem is that in general real life problems may only be modeled by nonlinear systems. In this case, we only know how to describe the solutions globally (via nullclines). What happens around an equilibrium point remains a mystery so far. Here we propose the to discuss this problem. The main idea is to approximate a nonlinear system by a linear one (around the equilibrium point). Of course, we do hope that the behavior of the solutions of the linear system will be the same as the nonlinear one. This is the case most of the time (not all the time!).

Example. Consider the Van der Pol equation

This is a nonlinear equation. Let us translate this equation into a system. Set 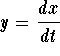. Then we have

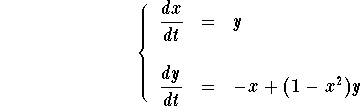
The equilibrium points reduce to the only point (0,0). Let us find the nullclines and the direction of the velocity vectors along them.

The x-nullcline is given by

Hence the x-nullcline is the x-axis.

The y-nullcline is given by

Hence the y-nullcline is the curve .

In the picture below we draw the nullclines and direction of the velocity vectors along them.

Note that the arrangement of these curves tell us that the solutions ``circles'' around the origin. But it is not clear whether the solutions circle and dye at the origin, circle away from the origin, or keep on circling periodically. A very rough approach to this problem suggests that if we rewrite the term as , then when (x,y) is close to (0,0), the term is very small compared to -x+y. Hence a close system to the original nonlinear system is

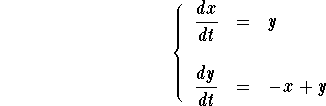
which happens to be a linear system. The eigenvalues of this system are 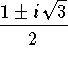. Hence the solutions of the linear system spiral away from the origin (since the real part is positive). So we suggest that the solutions of nonlinear system spiral away from the origin (look at the picture below)

The solution started close to the equilibrium point, then it moved away. Notice that in this case, the trajectory is getting close to what looks like a cycle. To better see this, let us consider the graphs of the function x(t) and y(t):

and

So what if we want to generalize this to different systems. Is there a technique that mimic what we did? The answer is yes. It is called linearization.

Linearization Technique.

Consider the autonomous system

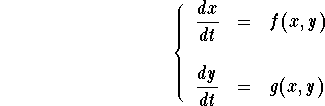
And assume that is an equilibrium point. So we would like to find the closest linear system when (x,y) is close to . In order to do that we need to approximate the functions f(x,y) and g(x,y) when (x,y) is close to . This is a similar problem to approximating a real valued function by its tangent (around a point of course). From multivariable calculus, we get

and

when (x,y) is close to . Then the nonlinear system may be approximated by the system

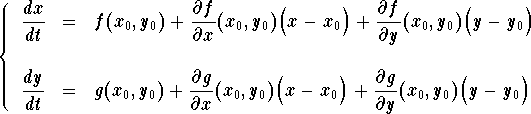
But since is an equilibrium point, then we have . Hence we have

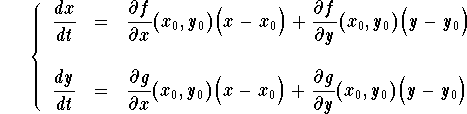
This is a linear system. Its coefficient matrix is

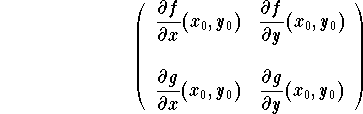
This matrix is called the Jacobian matrix of the system at the point .

Summary of the linearization technique.
Consider the autonomous system

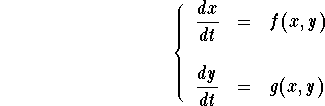
and an equilibrium point.

Find the partial derivatives

Write down the Jacobian matrix

Find the eigenvalues of the Jacobian matrix.

Deduce the fate of the solutions around the equilibrium point from the eigenvalues. For example,

if the eigenvalues are negative or complex with negative real part, then the equilibrium point is a sink (that is all the solutions will dye at the equilibrium point). Note that if the eigenvalues are complex, then the solutions will spiral around the equilibrium point.

If the eigenvalues are positive or complex with positive real part, then the equilibrium point is a source (that is all the solutions will move away from the equilibrium point). Note that if the eigenvalues are complex, then the solutions will spiral away from the equilibrium point.

If the eigenvalues are real number with different sign (one positive and one negative), then the the equilibrium point is a saddle. In fact, there will be two solutions which approach the equilibrium point as , and two more solutions which approach the equilibrium point as . For the linear system theses solutions are lines, but for the nonlinear system they are not in general. These four solutions are called separatrix.

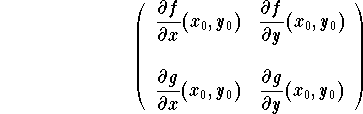
Remark. When dealing with an autonomous system without prior knowledge of the equilibrium point, then we advice to first find the Jacobian matrix and plug the values for every equilibrium point. This way you don't repeat the calculations over and over again.

Example. Consider the equation of the pendulum

where is the damping coefficient. See the picture below.

The equivalent system is

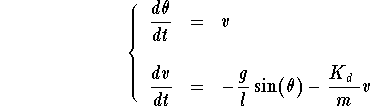
The equilibrium points are , where . The angles , for , correspond to the pendulum at its lowest position, while , for , correspond to the pendulum at its highest position. The Jacobian matrix of the system

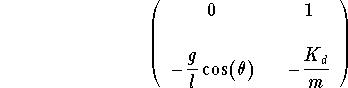
Let us concentrate on the equilibrium positions (0,0) and .

For (0,0), the Jacobian matrix is

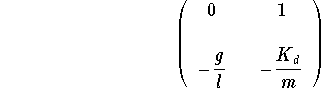
For the sake of illustration let us fix the parameters. For example,

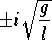if we take (undamped pendulum), then the eigenvalues are which implies that the mass will oscillate around the lowest position in a periodic fashion.

If (dumped pendulum), m=1, and l=1. Then the eigenvalues are

Since the real part is negative, the solutions will sink (dye) while oscillating around the equilibrium point. Here we have the same behavior for the linear and nonlinear system.

For , the Jacobian matrix is

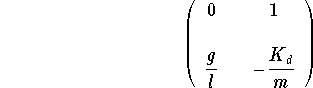
The eigenvalues are

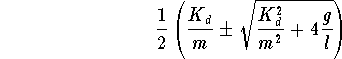
Clearly we have two real eigenvalues with one positive and one negative. So the solutions will always get away from the equilibrium position except along one curve (the separatrix).

More on the pendulum may be found by clicking here.

For more examples, click on Example.

[Differential Equations] [First Order D.E.] [Geometry] [Algebra] [Trigonometry ] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Copyright � 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour