The Radius of Convergence of Series Solutions

In the last section we looked at one of the easiest examples of a second-order linear homogeneous equation with non-constant coefficients: Airy's Equation

y''-t y=0,

which is used in physics to model the defraction of light.

We found out that

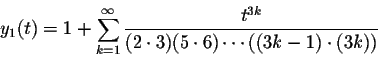
$\begin{displaymath}y_1(t)= 1+\sum_{k=1}^\infty \frac{t^{3k}}{(2\cdot 3)(5\cdot 6)\cdots((3k-1)\cdot (3k))}\end{displaymath}$

and

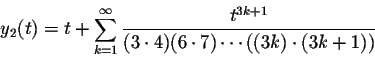
$\begin{displaymath}y_2(t)=t+\sum_{k=1}^\infty\frac{t^{3k+1}}{(3\cdot 4)(6\cdot 7)\cdots((3k)\cdot (3k+1))}\end{displaymath}$

form a fundamental system of solutions for Airy's Differential Equation.

The natural questions arise, for which values of t these series converge, and for which values of t these series solve the differential equation.

The first question could be answered by finding the radius of convergence of the power series, but it turns out that there is an elegant Theorem, due to Lazarus Fuchs (1833-1902), which solves both of these questions simultaneously.

Fuchs's Theorem. Consider the differential equation

y''+p(t) y'+q(t) y=0

with initial conditions of the form y(0)=y₀ and y'(0)=y'₀.

Let r>0. If both p(t) and q(t) have Taylor series, which converge on the interval (-r,r), then the differential equation has a unique power series solution y(t), which also converges on the interval (-r,r).

In other words, the radius of convergence of the series solution is at least as big as the minimum of the radii of convergence of p(t) and q(t).

In particular, if both p(t) and q(t) are polynomials, then y(t) solves the differential equation for all $t\in\Bbb R$ .

Since in the case of Airy's Equation p(t)=0 and q(t)=-t are both polynomials, the fundamental set of solutions y₁(t) and y₂(t) converge and solve Airy's Equation for all $t\in\Bbb R$ .

Let us look at some other examples:

Hermite's Equation of order n has the form

y''-2ty'+2ny=0,

where n is usually a non-negative integer. As in the case of Airy's Equation, both p(t)=-2t and q(t)=2n are polynomials, thus Hermite's Equation has power series solutions which converge and solve the differential equation for all $t\in\Bbb R$ .

Legendre's Equation of order $\alpha$ has the form

$\begin{displaymath}(1-t^2)y''-2ty' +\alpha(\alpha+1)y=0,\end{displaymath}$

where $\alpha$ is a real number.

Be careful! We have to rewrite this equation to be able to apply Fuchs's Theorem. Let's divide by 1-t²:

$\begin{displaymath}y''-\frac{2t}{1-t^2}y'+ \frac{\alpha(\alpha+1)}{1-t^2}y=0.\end{displaymath}$

Now the coefficient in front of y'' is 1 as required.

What is the radius of convergence of the power series representations of

$\begin{displaymath}p(t)=-\frac{2t}{1-t^2} \mbox { and } q(t)= \frac{\alpha(\alpha+1)}{1-t^2}?\end{displaymath}$

(The center as in all our examples will be t=0.) We really have to investigate this question only for the function

$\begin{displaymath}f(t)=\frac{1}{1-t^2},\end{displaymath}$

since multiplication by a polynomial (-2t, and $\alpha(\alpha+1)$ , respectively) does not change the radius of convergence.

The geometric series

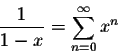
$\begin{displaymath}\frac{1}{1-x}=\sum_{n=0}^\infty x^n\end{displaymath}$

converges when -1<x<1. If we substitute x=t², we obtain the power series representation we seek:

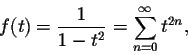
$\begin{displaymath}f(t)=\frac{1}{1-t^2}=\sum_{n=0}^\infty t^{2n},\end{displaymath}$

which will be convergent when -1<x=t²<1, i.e., when -1<t<1. Thus both

$\begin{displaymath}p(t)=-\frac{2t}{1-t^2} \mbox { and } q(t)= \frac{\alpha(\alpha+1)}{1-t^2}\end{displaymath}$

will converge on the interval (-1,1). Consequently, by Fuchs's result, series solutions to Legendre's Equation will converge and solve the equation on the interval (-1,1).

Bessel's Equation of order $\alpha$ has the form

$\begin{displaymath}t^2y''+ty' +(t^2-\alpha^2)y=0,\end{displaymath}$

where $\alpha$ is a non-negative real number.

Once again we have to be careful! Let's divide by t²:

$\begin{displaymath}y''-\frac{1}{t}y'+ \frac{t^2\alpha^2}{t}y=0.\end{displaymath}$

Now the coefficient in front of y'' is 1 as required by Fuchs's Theorem.

The function 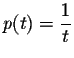$p(t)=\displaystyle\frac{1}{t}$ has a singularity at t=0, thus p(t) fails to have a Taylor series with center t=0. Consequently, Fuchs's result does not even guarantee the existence of power series solutions to Bessel's equation.

As it turns out, Bessel's Equation does indeed not always have solutions, which can be written as power series. Nevertheless, there is a method similar to the one presented here to find the solutions to Bessel's Equation. If you are interested in Bessel's Equation, look up the section on "The Method of Frobenius" in a differential equations or advanced engineering mathematics textbook.

[Back] [Next] [Algebra] [Trigonometry] [Complex Variables] [Calculus] [Differential Equations] [Matrix Algebra]

S.O.S. MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Helmut Knaust
1998-07-05