 Method of Variation of Parameters
Method of Variation of Parameters  Method of Variation of Parameters
Method of Variation of Parameters

This method has no prior conditions to be satisfied. Therefore, it
may sound more general than the previous method. We will see that
this method depends on integration while the previous one is purely
algebraic which, for some at least, is an advantage.
Consider the equation
![]()
In order to use the method of variation of parameters we need to know
that ![]() is a set of fundamental solutions of the associated
homogeneous equation y'' + p(x)y' + q(x)y = 0. We know that, in
this case, the general solution of the associated
homogeneous equation is
is a set of fundamental solutions of the associated
homogeneous equation y'' + p(x)y' + q(x)y = 0. We know that, in
this case, the general solution of the associated
homogeneous equation is ![]() . The idea behind
the method of variation of parameters is to look for a particular
solution such as
. The idea behind
the method of variation of parameters is to look for a particular
solution such as
![]()
where ![]() and
and ![]() are functions. From this, the method got its name.
are functions. From this, the method got its name.
The functions ![]() and
and ![]() are solutions to the system
are solutions to the system
![]() ,
,
which implies
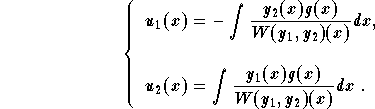 ,
,
where ![]() is the
wronskian
of
is the
wronskian
of ![]() and
and ![]() .
Therefore, we have
.
Therefore, we have
![]()
Summary:Let us summarize the steps to follow in applying this method:
![]() a set of fundamental solutions of the
associated homogeneous equation
a set of fundamental solutions of the
associated homogeneous equation
![]() ;
; ![]() ;
; ![]() and
and ![]() ;
;
![]() and
and ![]() into the equation giving the particular
solution.
into the equation giving the particular
solution.
Example: Find the particular solution to
![]()
Solution: Let us follow the steps:
![]()
![]() ;
;
![]()
Using techniques of integration, we get
![]() ;
;
![]() ,
,
or
![]()
Remark: Note that since the equation is linear, we may still split if necessary. For example, we may split the equation
![]() ,
,
into the two equations
![]()
then, find the particular solutions ![]() for (1) and
for (1) and ![]() for (2),
to generate a particular solution for the original equation by
for (2),
to generate a particular solution for the original equation by
![]()
There are no restrictions on the method to be used to find ![]() or
or
![]() . For example, we can use the
method of undetermined
coefficients to find
. For example, we can use the
method of undetermined
coefficients to find ![]() , while for
, while for ![]() , we are only left with the
variation of parameters.
, we are only left with the
variation of parameters.

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Mohamed Amine Khamsi