The Wronskian
The Wronskian
Let 
and 
be two differentiable functions. We will say that
and are proportional if and only if there exists a
constant C such that 
. Clearly any function is
proportional to the zero-function. If the constant C is not
important in nature and we are only interested into the proportionality
of the two functions, then we would like to come up with an equivalent
criteria. The following statements are equivalent:
and are proportional;
is a constant function;
;
.
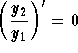Therefore, we have the following:
and are not proportional if, and only if, 
.
Define the Wronskian 
of and to be 
, that is
The following formula is very useful (see reduction of order technique):
Remark: Proportionality of two functions is equivalent to their linear dependence. Following the above discussion, we may use the Wronskian to determine the dependence or independence of two functions. In fact, the above discussion cannot be reproduced as is for more than two functions while the Wronskian does....