 Euler-Cauchy Equations
Euler-Cauchy Equations

An Euler-Cauchy equation is
where b and c are constant numbers. Let us consider the change of
variable
x = et.
Then we have
The equation (EC) reduces to the new equation
We recognize a second order differential equation with constant
coefficients. Therefore, we use the previous sections to solve it.
We summarize below all the cases:
- (1)
- Write down the characteristic equation
- (2)
- If the roots r1 and r2 are distinct real numbers,
then the general solution of (EC) is given by
y(x) = c1 |x|r1 + c2 |x|r2.
- (2)
- If the roots r1 and r2 are equal (r1 = r2), then
the general solution of (EC) is
- (3)
- If the roots r1 and r2 are complex numbers, then the
general solution of (EC) is
where
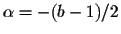 and
and
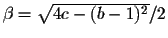 .
.
Example: Find the general solution to
Solution: First we recognize that the
equation is an Euler-Cauchy equation, with b=-1 and c=1.
- 1
- Characteristic equation is
r2 -2r + 1=0.
- 2
- Since 1 is a double root, the general solution is

[Differential Equations]
[First Order D.E.]
[Second Order D.E.]
[Geometry]
[Algebra]
[Trigonometry ]
[Calculus]
[Complex Variables]
[Matrix Algebra]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Author: Mohamed
Amine Khamsi
Copyright � 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
 Euler-Cauchy Equations
Euler-Cauchy Equations  Euler-Cauchy Equations
Euler-Cauchy Equations 

 S.O.S MATHematics home page
S.O.S MATHematics home page 