First Order Linear Equations

A first order linear differential equation has the following form:

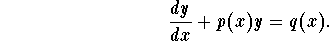
The general solution is given by

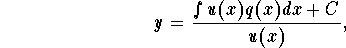
where

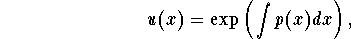
called the integrating factor. If an initial condition is given, use it to find the constant C.

Here are some practical steps to follow:

1.

If the differential equation is given as

,

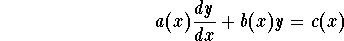rewrite it in the form

,

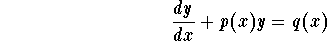where

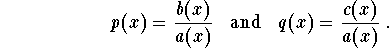
2.

Find the integrating factor

.

3.

Evaluate the integral

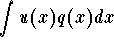
4.

Write down the general solution

.

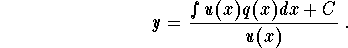5.

If you are given an IVP, use the initial condition to find the constant C.

Example: Find the particular solution of:

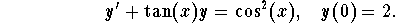
Solution: Let us use the steps:

Step 1: There is no need for rewriting the differential equation. We have

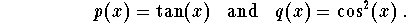
Step 2: Integrating factor

.

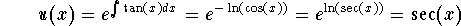Step 3: We have

.

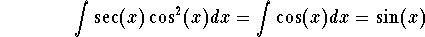Step 4: The general solution is given by

.

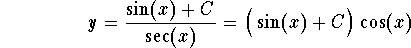Step 5: In order to find the particular solution to the given IVP, we use the initial condition to find C. Indeed, we have

.

Therefore the solution is

.

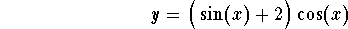Note that you may not have to do the last step if you are asked to find the general solution (not an IVP).

If you would like more practice, click on Example.

[Differential Equations] [Separable Equations] [Next Example] [Geometry] [Algebra] [Trigonometry ] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Copyright � 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour