 Techniques of Differentiation
Techniques of Differentiation
 Techniques of Differentiation
Techniques of Differentiation
Maybe the
easiest and most useful formulas are the ones that say that the
derivative is linear:

Example. For
P(x) = 1-2x + 3x4 -5 x6, we have
The next two formulas are the most powerful ones. They deal with the derivative of a product and a quotient. They are commonly called the product rule and the quotient rule. We have

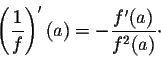
Before we discuss the derivative of trigonometric functions, let
us stop here and reflect a little bit more on polynomial
functions. Indeed, we saw that the derivative of a polynomial
function is also a polynomial function. So we can take another
derivative and generate a new function. This function is called
the second derivative. We can keep doing this as long as we
want to. The functions obtained are called higher derivatives.
The common notations used for them are

Exercise 1. Find the derivative of the function
Exercise 2. Find the derivative of
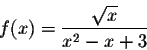
Exercise 3. Solve the equation
 when
when
Exercise 4. Find the points on the graph of y = x3/2 - x1/2 at which the tangent line is parallel to the line y+2x = 1. Also find the points on the same graph at which the tangent line is perpendicular to the line y-x = 3.
 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Mohamed A. Khamsi