ON INVERSE FUNCTIONS
Composition of Functions
Suppose the rule of function f(x) is 
and the rule of function g(x) is 
. Suppose now that you want to "leapfrog" the functions as follows: Take a 2 in the domain of f and link it to 9 with the f(x) rule, and then take the 9 and link it to 157 with the g(x) rule. This is a lot of work and you would rather just work with one function, a function rule that would link the 2 directly to the 157.
Since the g function operates on f(x), we can write the composition as g(f(x)). Let’s call the new function h(x) = g(f(x)). You can simplify from the inside out or the outside in.
Inside Out: 
Let’s check to see if the above function will link 2 directly to 157.
It does.
Outside In: 
You can see that it is the same as the function we derived from the inside out.
The following is an example of finding the composition of two functions.
Example 1: Find 
and 
if 
and 
.
Solution - :
Inside Out:
The composition function is equal to 
Outside In:
Check:
and the function f(x) links the 25 to the number 668 because 
.
Let’s see if the new function, let’s call it h(x), will link the 5 directly to the 668. 
It does and the new composition function can be written
Solution - 
:
Inside Out:
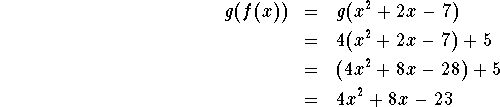
The composition function is equal to 
Outside In:
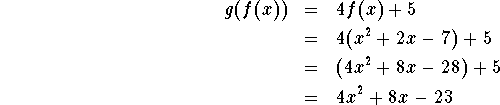
Check:
and the function g(x) links the 1 to the number 9 because
.
Let’s see if the new function, let’s call it h(x), will link the 2 directly to the 9.
It does and the new composition function can be written
Students often ask why are these functions different. They assume that the new function created by f(g(x)) is the same function created by g(f(x)).
Wrong Assumption! Sometimes they are equal, but most of the time, these functions are different.
Review another example of finding the composition of functions.
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Author:Nancy Marcus