Absolute Value Inequalities

The ``forget the minus sign" definition of the absolute value is useless for our purposes. Instead, we will mostly use the geometric definition of the absolute value:

The absolute value of a number measures its distance to the origin on the real number line.

Since 5 is at 5 units distance from the origin 0, the absolute value of 5 is 5, |5|=5

Since -5 is also at a distance of 5 units from the origin, the absolute value of -5 is 5, |-5|=5:

We are ready for our first inequality. Find the set of solutions for

|x|<5.

Translate into English: we are looking for those real numbers x whose distance from the origin is less than 5 units.

Obviously we are talking about the interval (-5,5):

What about the solutions to $\vert x\vert\geq 2$ ?

In English: which numbers, x, are at least 2 units away from the origin? On the left side, real numbers less than or equal to -2 qualify, on the right all real numbers greater than or equal to 2:

We can write this interval notation as

$\begin{displaymath}(-\infty,-2]\cup[2,\infty).\end{displaymath}$

What is the geometric meaning of |x-y|?

|x-y| is the distance between x and y on the real number line.

Consider the example |(-4)-3|. The distance on the real number line between the points -4 and +3 is 7, thus

|(-4)-3|=7.

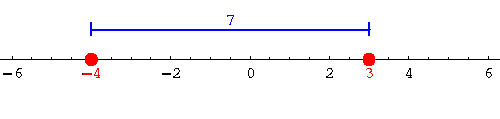
Let's find the solutions to the inequality:

$\begin{displaymath}\vert x-2\vert\leq 1.\end{displaymath}$

In English: Which real numbers are not more than 1 unit apart from 2?

We're talking about the numbers in the interval [1,3].

What about the example

$\begin{displaymath}\vert x+1\vert\geq 3?\end{displaymath}$

Let's rewrite this as

$\begin{displaymath}\vert x-(-1)\vert\geq 3,\end{displaymath}$

which we can translate into the quest for those numbers x whose distance to -1 is at least 3.

The set of solutions is

$\begin{displaymath}(-\infty,-4]\cup[2,\infty).\end{displaymath}$

With a little bit of tweaking, our method can also handle inequalities such as

|2x-5|<2.

We first divide both sides by 2. Note that absolute values interact nicely with multiplication and division:

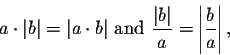
$\begin{displaymath}a\cdot \vert b\vert=\vert a\cdot b\vert \mbox{ and }\frac{\vert b\vert}{a}=\left\vert\frac{b}{a}\right\vert,\end{displaymath}$

as long as a is positive.

Thus we obtain

$\begin{displaymath}\left\vert\frac{2x-5}{2}\right\vert<\frac{2}{2};\end{displaymath}$

after simplification, we get the inequality

$\begin{displaymath}\left\vert x-\frac{5}{2}\right\vert<1,\end{displaymath}$

asking the question, which numbers are less than 1 unit apart from $\frac{5}{2}.$

So the original inequality has as its set of solutions the interval $\left(\frac{3}{2},\frac{7}{2}\right)$ .

Consider the example

$\begin{displaymath}\vert\pi-3x\vert\geq 2.\end{displaymath}$

Let's divide by 3:

$\begin{displaymath}\left\vert\frac{\pi}{3}-x\right\vert\geq \frac{2}{3},\end{displaymath}$

which is the same as

$\begin{displaymath}\left\vert x-\frac{\pi}{3}\right\vert\geq \frac{2}{3}.\end{displaymath}$

Which numbers have distance at least $\frac{2}{3}$ from $\frac{\pi}{3}$ ? The set of solutions is given by

$\begin{displaymath}\left(-\infty,\frac{\pi}{3}-\frac{2}{3}\right]\cup\left[\frac{\pi}{3}+\frac{2}{3},+\infty\right).\end{displaymath}$

Our method fails for more contrived examples.

Let us consider the inequality

|x-3|<2x-4

It's back to basic algebra with a twist.

The standard definition for the absolute value function is given by:

$\begin{displaymath}\vert x\vert=\left\{\begin{array}{ll} x &\mbox{, if }x\geq 0\\ -x &\mbox{, if }x<0 \end{array} \right.\end{displaymath}$

Thus we can get rid of the $\vert\mbox{ }\vert$ sign in our inequality if we know whether the expression inside, x-3, is positive or negative.

We will do exactly that!

Let's first consider only those values of x for which $x-3\geq 0$ :

Case 1: $x\geq3$

In this case we know that |x-3|=x-3, so our inequality becomes

x-3<2x-4

Solving the inequality, we obtain

x>1.

We have found some solutions to our inequality:

x is a solution if $x\geq3$ and x>1 at the same time! We're talking about numbers $x\geq3$ .

What if x-3<0?

Case 2: x<3

This time x-3<0, so |x-3|=-(x-3)=3-x, so our inequality reads as

3-x<2x-4.

Applying the standard techniques, this can be simplified to

$\begin{displaymath}x>\frac{7}{3}.\end{displaymath}$

Our inequality has some more solutions:

Under our case assumption x<3, solutions are those real numbers which satisfy $x>\frac{7}{3}$ .

We're talking about numbers in the interval

$\begin{displaymath}\left(\frac{7}{3},3\right)\end{displaymath}$

Combining the solutions we found for both cases, we conclude that the set of solutions for the inequality

|x-3|<2x-4

are the numbers in the interval

$\begin{displaymath}\left(\frac{7}{3},+\infty\right).\end{displaymath}$

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Helmut Knaust

Absolute Value Inequalities

Exercise 1.

Answer.

Exercise 2.

Answer.

Exercise 3.

Answer.

Exercise 4.

Answer.

Exercise 5.

Answer.