- notation:
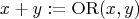
,
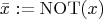
,
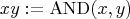
, 1:=TRUE, 0:=FALSE.
- Let

be a Boolean function of

-variables, i.e.
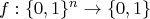
.
- minterm:= any product (AND) of

literals (complemented or uncomplemented). e.g,
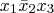
is a minterm in 3 variables
-
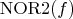
is the minimum number of 2-input NOR gates required to represent a given function

. For instance,
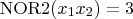
.
Let
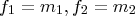
, where
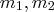
are minterms that are **co-prime** (i.e,
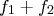
can't be minimized further. In other words,
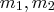
are prime implicants of
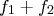
). For instance,
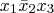
and
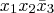
are co-prime
Then, is the following true?
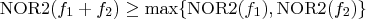
[i.e, adding two coprime minterms can't yield a 2-input NOR circuit with fewer gates]
I think it is true but I can't think of a proof. Any ideas on how to start proving it?



