Pan Miroslav wrote:
I got some troubles proving following theorems:
1) In linear regression model with DEPENDENT normally distributed errors (with covariance matrix
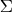
) the maximum likelihood estimation of

gives
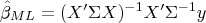
2) Let
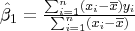
be estimated by least squares method, let
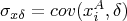
,

,

.
Show that
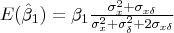
My progress - in the second one, simply putting all the things I know to the result and hoping that it will give expectation of the
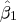
simply did not work. For the first one I don't know what to try, because I'm not even sure how the likelihood function looks like when we got dependent errors.
(1) Recall the probability density function of multivariate normal distribution
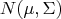
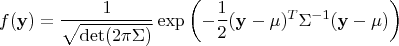
(2) What are
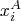
and
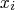
? What is
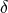
?
Anyway, split

where
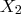
contains all the other independent variables that we ignore and write

. Expand out
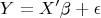
in the formula for ordinary least-square and take (conditional) expectation (so the

disappears). The result is the so-called
omitted variable (bias) formula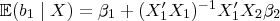
which has an intuitive description --- the bias
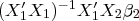
is precisely the weighted proportion of the omitted variables
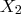
that are "explained" by the variables
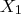
we included.



