If you remember back, you know that for 0, 1, 5, and 6 when you square them, the resulting last digit is equal to the original last digit. In other bases you can find such numbers as well, for example, in base 6 if something ends in 0, 1, 3, or 4 then the square ends in the same digit.
If you were to graph the number of digits with this property for each base it would oscillate around a lot, but you would begin to notice that it would go up every time you hit a new product of consecutive primes, so 2, 3, 4, 5, have only two digits that do this, then 6 has 4 of them, keeping going, 30 is the next jump and has 8, in fact, when you get the product of the first k primes, you will see that exactly
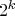
digits have this property, and this is the smallest value for which this is true.
For this problem show
1 (warm-up) This formula holds in general for the product of the first k primes
2 (harder) show that the product of the first k consecutive primes is the smallest value for which you get
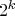
3 (hardest) show that, in fact, all values for the number of digits is even, and provide a formula for an arbitrary