Logic minimization via 2 inputs NOR gates: Is it monotone w.

M.A · **Joined:** Thu, 26 Jul 2007 19:08:57 UTC **Posts:** 68

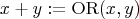
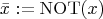
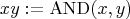
- notation: $x+y:=\mbox{OR}(x,y)$ , $\bar x:=\mbox{NOT}(x)$ , $xy:=\mbox{AND}(x,y)$ , 1:=TRUE, 0:=FALSE.

- Let

be a Boolean function of

-variables, i.e. $f: \{0,1\}^n \to \{0,1\}$ .
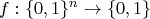
- minterm:= any product (AND) of

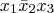
literals (complemented or uncomplemented). e.g, $x_1 \bar x_2 x_3$ is a minterm in 3 variables

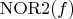
- $\mbox{NOR2}(f)$ is the minimum number of 2-input NOR gates required to represent a given function

. For instance, $\mbox{NOR2}(x_1 x_2)=3$ .

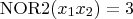
Let f_1= m_1, f_2=m_2

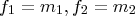
, where

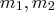
are minterms that are **co-prime** (i.e, f_1+f_2

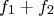
can't be minimized further. In other words, m_1,m_2

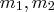
are prime implicants of f_1+f_2

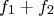
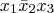
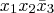
). For instance, $x_1 \bar x_2 x_3$ and $x_1 x_2 \bar x_3$ are co-prime

Then, is the following true?
$\mbox{NOR2}(f_1+f_2)\ge \mbox{max}\{ \mbox{NOR2}(f_1), \mbox{NOR2}(f_2) \}$

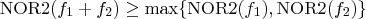
[i.e, adding two coprime minterms can't yield a 2-input NOR circuit with fewer gates]

I think it is true but I can't think of a proof. Any ideas on how to start proving it?

S.O.S. Mathematics CyberBoard

Logic minimization via 2 inputs NOR gates: Is it monotone w.

Who is online