For the first quadratic, the roots are:
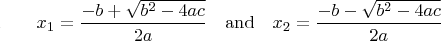
and likewise, for the second the quadratic, the roots are:
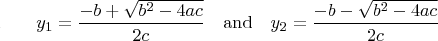
and thus we obtain the relationships:
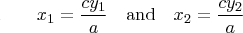
edit: a/c -> c/a
| S.O.S. Mathematics CyberBoard http://417773.os285nnd.asia/CBB/ |
|
| quadratic equations http://417773.os285nnd.asia/CBB/viewtopic.php?f=1&t=19571 |
Page 1 of 1 |
| Author: | kasheee [ Fri, 25 Nov 2005 00:06:46 UTC ] |
| Post subject: | quadratic equations |
ax^2+bx+c=0 and cx^2+bx+a=0 are 2 quadratic equations with their coefficients in reverse order. Find the relationship between the roots of the 2 equations. Thanks. |
|
| Author: | Matt [ Fri, 25 Nov 2005 00:11:11 UTC ] |
| Post subject: | |
For the first quadratic, the roots are: 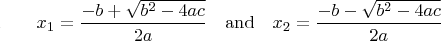 and likewise, for the second the quadratic, the roots are: 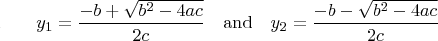 and thus we obtain the relationships: 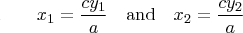 edit: a/c -> c/a |
|
| Author: | jinydu [ Fri, 25 Nov 2005 00:30:36 UTC ] |
| Post subject: | Re: quadratic equations |
kasheee wrote: ax^2+bx+c=0 and cx^2+bx+a=0 are 2 quadratic equations with their coefficients in reverse order. Find the relationship between the roots of the 2 equations. Thanks. To see very quickly why the roots of those quadratics must be inverses of each other, divide both sides of both equations by x, then use the substitution 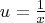 on one and only one of the equations (your choice which one). on one and only one of the equations (your choice which one).As I learned on this very board, polynomial equations of degree n (where n is even) with palindromic (first-to-last the same as last-to-first) coefficients can be reduced to polynomial equations of degree 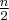 using the substitution using the substitution 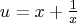 . .
|
|
| Author: | Matt [ Fri, 25 Nov 2005 00:48:01 UTC ] |
| Post subject: | Re: quadratic equations |
jinydu wrote: the roots of those quadratics must be inverses of each other In other words, two more relationships you can derive are: 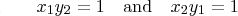 (using the notation of my first post above). |
|
| Author: | Soroban [ Fri, 25 Nov 2005 02:35:05 UTC ] |
| Post subject: | Re: quadratic equations |
Hello, kasheee! Quote: 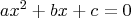 and and 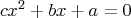 are two quadratic equations are two quadratic equations. . with their coefficients in reverse order. Find the relationship between the roots of the two equations. The roots of 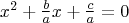 have a product of have a product of 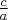 The roots of 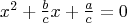 have a product of have a product of 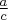 Therefore, the product of all four roots is 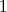 . .
|
|
| Author: | kasheee [ Sat, 17 Dec 2005 20:23:15 UTC ] |
| Post subject: | |
Looking back at the answeras i have received in the past I noticed this question I posted. Isn't a*x1=y1*c? Not (x1=a*y1)/c Thanks. |
|
| Author: | Matt [ Sat, 17 Dec 2005 21:30:20 UTC ] |
| Post subject: | |
kasheee wrote: Looking back at the answeras i have received in the past I noticed this question I posted. Isn't a*x1=y1*c? Not (x1=a*y1)/c Indeed, kashee. I'm surprised nobody pointed that out earlier. Thanks. |
|
| Author: | kasheee [ Sun, 30 Jul 2023 16:56:36 UTC ] |
| Post subject: | Re: quadratic equations |
Looking back at this question I posted twenty years ago, could we also relates x1 to y2, and x2 to y1? Thanks. |
|
| Author: | kasheee [ Mon, 31 Jul 2023 20:13:50 UTC ] |
| Post subject: | Re: quadratic equations |
Not neccessary to reply. I can see my question has been answered. |
|
| Page 1 of 1 | All times are UTC [ DST ] |
| Powered by phpBB® Forum Software © phpBB Group http://www.phpbb.com/ |
|